
Canadian
Mathematical
Society
Mini Courses
The CMS is organizing mini-courses to add more value to meetings and make them attractive for students and researchers to attend. The mini-courses will be held on Friday, May 31 and include topics suitable for graduate students, postdocs, and other interested parties.
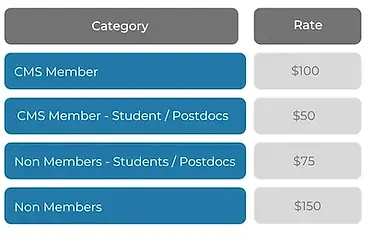
Registration fees for the mini courses are:
Unveiling Infinite Symmetries
Mini Course on Algebraic Structures of Generalized Kac-Moody Type
Friday, May 31 | 9am - 12pm | 1pm - 4pm
Saturday June 1 & Sunday June 2 | Scientifc Session
Organizers
Abid Ali (University of Saskatchewan)
Lisa Carbone (Rutgers University)
Steven Rayan (University of Saskatchewan)
Lectures
Lisa Carbone (Rutgers University)
Elizabeth Jurisich (The College of Charleston)
Maryam Khaqan (University of Toronto)
Scott Murray (Rutgers University)
Infinite-dimensional Lie algebras, including Kac-Moody algebras, Monstrous Lie algebras, and more
generally, Borcherds algebras, play a crucial role in various branches of mathematics and theoretical
physics. The mini-course will cover fundamental concepts related to these infinite-dimensional Lie
algebras and their associated groups, share the latest developments on these topics, and discuss
potential future projects on the new constructions.
This mini-course will be followed up by a scientific session taking place from Saturday, June 1 to Monday, June 3.
DNA topology is the study of the geometry (supercoiling) and topology (knotting and linking) of DNA. Knots and links in DNA are known to obstruct normal cellular processes and geometric factors such as the amount of writhe or supercoiling are known to affect the formation of entanglements in DNA. Enzymes that act on DNA to cut and reconnect the DNA are nature’s solution for removing these
topological obstructions. Polymer models have proved useful for geometric modeling of DNA conformations and methods from knot theory have enabled the characterization of entanglements and the results of enzyme action. Topological methods including tangle analysis, braid theory, classical and quantum knot invariants, and Floer homology can be successfully applied to analyze reactions and
characterize entangled structures.
The mini-course on DNA topology will be structured as follows.
1. Discussion of motivational problems from DNA experiments [enzyme action on DNA, DNA packing]
2. Overview of knot theoretic foundations and methodology [skein relations, knot polynomials, tangle and braid techniques, homology-theoretic strategies]
3. Hands-on computational tools crash-course demonstrating several packages, programs, and techniques. [Participants will learn about tools such as the Knot Theory package in Sage, KnotPlot, lattice knot simulations, and other computational tools and databases.]
This Mini-course is sponsored by the PIMS CRG on Novel Techniques in Low Dimension https://www.pims.math.ca/programs/scientific/collaborative-research-groups/novel-techniques-low-dimension-floer-homology
Applied Topology:
DNA Topology
Friday, May 31 | 9am - 12pm
Organizers
Ryan Budney (University of Victoria)
Allison Moore (Virginia Commonwealth University)
Koya Shimokawa (Ochanomizu University)
Chris Soteros (USask)
Mariel Vazquez (UCDavis)
Partial funding may be available for students, postdocs, and early-career researchers to attend the Applied Topology minicourses. To receive more information and apply for this opportunity, please fill out this google form. For full consideration, please apply by May 1 using this form: https://forms.gle/v5FEVmcYC4w2nyXw5
Applied Topology: Persistent Homology
Friday, May 31 | 1pm - 4pm
Organizers
Ryan Budney (University of Victoria)
Allison Moore (Virginia Commonwealth University)
Koya Shimokawa (Ochanomizu University)
Chris Soteros (USask)
Mariel Vazquez (UCDavis)
This Mini-course is sponsored by the PIMS CRG on Novel Techniques in Low Dimension https://www.pims.math.ca/programs/scientific/collaborative-research-groups/novel-techniques-low-dimension-floer-homology
Persistent Homology is an application of algebraic topology (filtered chain complexes) to statistics. Roughly speaking, one naturally associates filtered chain complexes to data in a variety of ways. Persistent homology is the structure of how the homology changes as the filtration evolves. Homology classes that exist for `long' or `big' regions in the filtration are deemed more significant than ones that exist for shorter or smaller periods. Research in persistent homology centres around issues such as 1) efficient computation for various filtration types, parallelization, etc, 2) theoretical significance of computations: stability or lack of it, and the ability to infer structure in the underlying data from computations, noise vs. signal.
The mini-course on Persistent Homology will be structured as follows:
1. Discussion of motivating examples and basic ideas from algebraic topology: homology, manifolds, Steenrod realization.
2. A sampling of a few different filtered chain complex types. Computation of persistent homology. Computer examples.
3. Basics of the theory: computational complexity, stability, signal vs. noise theorems, asymptotics.
CMS Student Committee
Writing Workshop
.png)
Friday, May 31 | 9am - 12pm
The Student Committee of the CMS (StudC) is organizing a writing workshop that will be held at the upcoming 2024 CMS Summer Meeting in Saskatoon. You are welcome to attend!
The objective of the workshop is to equip graduate students with effective approaches to research. There will be two presentations by two professors on “how to do research” and “how to present your research.” Everyone is welcome to attend, and there will be a free break!
This event is free of charge for those attending the meeting. It will take place on Friday, May 31st, from 9:00 to 12:00. Please fill in the following Google form if you are interested in participating (this is not mandatory to attend the workshop but facilitates the process): StudC Writing Workshop Form.