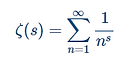Jeffery-Williams Prize Winner

Dr. Kumar Murty

Fields Institute

V. Kumar Murty received his doctorate from Harvard University in 1982 as a student of John Tate. In 1987, he was appointed Associate Professor at the University of Toronto, and in 1991 he was promoted to Full Professor. He was Chair of the Department of Mathematics at the University of Toronto during 2008-2013 and again from 2014-2017. He is currently the Director of the Fields Institute for Research in Mathematical Science.

ζ(3), log2, and π

The Riemann zeta function ζ(s) is defined by

​

​

for Re(s) > 1. Special values of the Riemann zeta function at integer points have been studied for centuries. In particular, Euler showed that at positive even integers 2k, we have          is rational. For example,                                and so on.

​

The values at positive odd integers have remained a mystery. In a posthumous 1785 paper, Euler conjectured that there are rational numbers α, β so that

​

After reviewing the fascinating story of how Euler came to this conclusion, we describe joint work with Payman Eskandari to show that this conjecture is inconsistent with conjectures in modern algebraic geometry. In particular, we use a conjecture of Grothendieck on periods of mixed motives to show that these three numbers ζ(3), log2, and π are in fact algebraically independent!

​

Thus, the value ζ(3) remains very enigmatic!