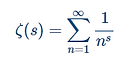Lauréat du prix Jeffery-Williams

Dr. Kumar Murty

Fields Institute

V. Kumar Murty a obtenu son doctorat de Harvard en 1982 en tant qu'étudiant de John Tate. En 1987, il a été nommé professeur agrégé au University of Toronto et, en 1991, il a été promu professeur titulaire. Il a été directeur du département de mathématiques du University of Toronto de 2008 à 2013, puis de 2014 à 2017. Il est actuellement directeur du Fields Institute for Research in Mathematical Science.

ζ(3), log2, et π

La fonction de Riemann zeta function ζ(s) est définie par

​

​

pour Re(s) > 1. Les valeurs spéciales à des points entiers de la fonction de Riemann zeta ont été étudiées pour des siècles. En particulier, Euler a démontré que pour les entiers pairs positifs 2k, nous avons          qui est rationnel. Par exemple,                             ,

et ainsi de suite.

​

Les valeurs des entiers impairs positifs sont restées un mystère. Dans un article posthume datant de 1785, Euler a conjecturé qu'il existe des nombres rationnels α, β tels que

​

​

Après voir revue l'histoire fascinate de la manière dont Euler est arrivé à cette conclusion, nous décrivons un travail commun avec Payman Eskandari pour montrer que cette conjecture est incompatible avec des conjectures de la géométrie algébrique moderne. En particulier, nous utilisons une conjecture de Grothendieck sur les périodes de motifs mixtes pour montrer que ces trois nombres sont en effet algébriquement indépendants!

​

Donc, la valeur ζ(3) reste très énigmatique!